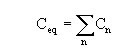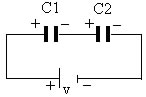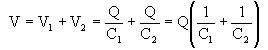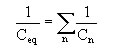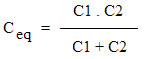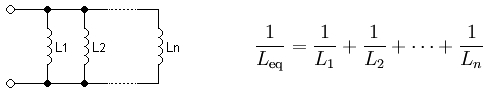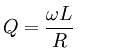Resistência

Os obstáculos impostos ao movimento eletrônico, conforme discussão qualitativa acima, são todos representados por uma propriedade mensurável, denominada resistência, e definida pela relação: onde, R = Resistência, V = Diferença de potencial aplicado (ou tensão), I = Corrente que circulará Exemplo: Uma resistência submetida a uma tensão de 110Volts, na qual circula uma corrente de 10 A possui o valor de: R = 110 / 10 = 11 ohms

R = V / I

Essa definição significa que, quando se aplica uma diferença de potencial (ddp), V, entre os extremos de um resistor, R, uma corrente, i, circulará, de tal modo que a relação acima será satisfeita.

Das variações da equação acima podemos deduzir:

A queda de tensão determinada por uma resistência R sob uma corrente I que a atravessa é: Exemplo: Sendo R = 100 ohms e I = 2,5 Ampéres, podemos determinar que V = 100 . 2,5 = 250 Volts	V = R . I
A corrente que passa por uma resistência R sob diferença de potencial V conhecidos, é: Exemplo: Sendo a diferença de potencial V = 110 Volts e a resistência R = 20 ohms, temos que a corrente que percorre a resistência é igual a   I = 110 / 20 = 5,5 Ampéres	I = V / R

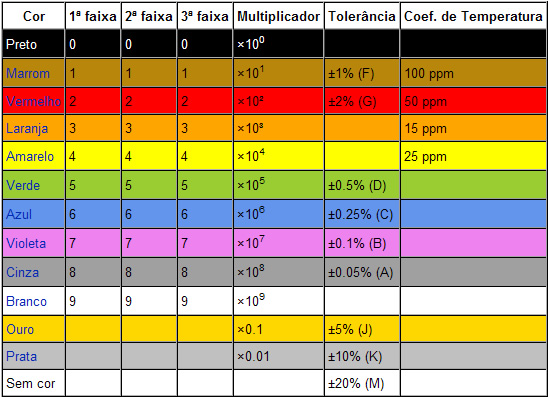
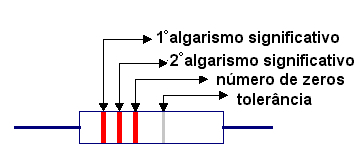
As grandezas relacionadas acima são facilmente mensuráveis com um ohmímetro (para medir R), com um voltímetro (para medir V) ou com um amperímetro (para medir I).

Resistores

Os resistores são componentes que apresentam resistência à passagem da corrente elétrica. Um resistor (chamado de resistência em alguns casos) é um dispositivo elétrico muito utilizado em eletrônica, com a finalidade de transformar energia elétrica em energia térmica (efeito joule), a partir do material empregado que pode ser por exemplo o carbono.

Um resistor ideal é um componente com uma resistência elétrica que permanece constante independentemente da tensão ou corrente elétrica que circular pelo dispositivo.

Os resistores podem ser fixos ou variáveis. Neste caso são chamados de potenciômetros (ou reostatos).O valor nominal é alterado ao girar um eixo ou deslizar uma alavanca.

O valor de um resistor de carbono pode ser facilmente determinado de acordo com as cores que apresenta na cápsula que envolve o material resistivo, ou então usando um instrumento denominado ohmímetro.

A identificação de 4 faixas é o esquema de codificação mais comumente usado em todos os resistores. Consiste de quatro faixas coloridas que são pintadas em torno do corpo do resistor. Os primeiros dois números são os primeiros dois dígitos significativos do valor da resistência, o terceiro é um multiplicador, e o quarto é o valor da tolerância. Cada cor corresponde a um certo número, mostrado na tabela abaixo. A tolerância para um resistor de 4 faixas será de 20%, 5%, ou 10% Unidades multiplicadoras: Kilo (K) = x 1.000 Mega (M) = x 100.000 Resistor de 2200 ohms = 2,2K Uma notação comum é indicar o multiplicador no lugar da vírgula. 2200 ohms = 2,2K = 2K2 3.900.000 = 3,9M = 3M9

Potência elétrica

A potência (unidade = Watts = W) é a razão entre o trabalho produzido e o tempo gasto. É a grandeza que define a quantidade de energia consumida por unidade de tempo.

Para cálculo, determina-se a potência dissipada através da fórmula: P = V . I
onde P = potência em Watts, V = tensão em Volts e I = corrente elétrica em Ampéres

Exemplo: Para um circuito de 110 Volts que consome a corrente de 4 Ampéres, temos uma potência consumida de 440 Watts.

Considerando que R = V / I, podemos calcular a potência dissipada em um circuito resistivo conhecendo-se sua resistência e mais a corrente ou a diferença de potencial aplicada:

Conhecendo-se a resistência e corrente elétrica

Conhecendo-se a tensão aplicada e a resistência

Com a tensão e corrente elétrica

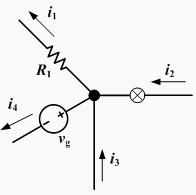
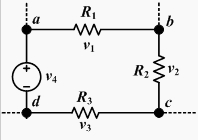
Lei de Joule

A corrente que atravessa um resistor produz calor. Essa energia térmica dissipada é medida em Joules, sendo determinada pela multiplicação da potência pelo tempo: 1 Watt = 1 Joule por segundo

Lei de Kirchhoff

1a Lei de Kirchhoff (Lei dos nós): A corrente que entra numa junção de circuito é igual a soma das correntes que saem desse mesmo circuito. Isso equivale a dizer para o exemplo ao lado, que    i2 + i3 = i1 + i4 Ainda, se convencionarmos que as correntes que entram em um nó são positivas e as que saem são negativas, equivale dizer que "A soma algébrica das correntes que entram em um ponto do circuito com as que saem do mesmo ponto, é zero"

2a Lei de Kirchhoff (lei das malhas ou das tensões) Em um circuito fechado, a soma das quedas de tensão nas resistências é igual a soma das tensões aplicadas. Isso equivale a dizer para o exemplo ao lado, que     v4 = v1 + v2 + v3 Também equivale a afirmar que A soma algébrica das quedas de tensão aplicadas ao circuito é igual a zero.

 

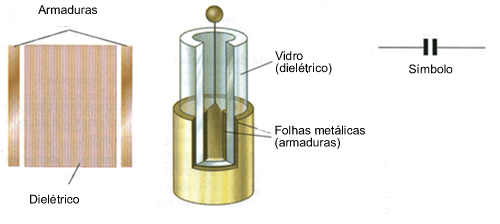
Capacitores

A busca por um dispositivo que armazenasse energia levou à descoberta do capacitor. É constituído de placas condutoras paralelas entre sí, porém separadas eletricamente uma das outras através de um dielétrico (material isolante).

O dielétrico pode ser um isolante qualquer como o vidro, a parafina, o papel e muitas vezes é o próprio ar. Nos diagramas de circuitos elétricos o capacitor é representado com o símbolo indicado na figura abaixo.

A propriedade que estes dispositivos têm de armazenar energia elétrica sob a forma de um campo eletrostático é chamada de capacitância (C) e é medida pelo divisão entre a quantidade de carga (Q) armazenada e a voltagem (V) que existe entre as placas.

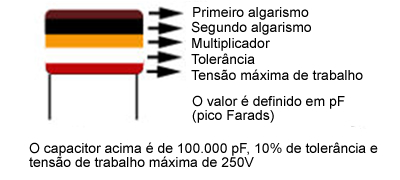
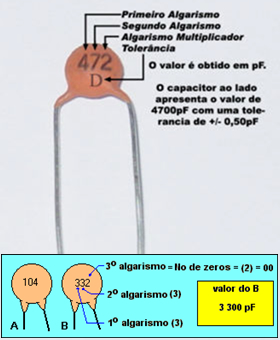
Um capacitor é fundamentalmente um armazenador de energia sob a forma de um campo eletrostático.

A unidade de medida de capacitância é o Farad (F), quando um Coulomb de carga causa uma diferença de potencial de um Volt (V) entre as placas. O Farad é uma unidade de medida considerada muito grande para circuitos práticos, por isso, são utilizados valores de capacitâncias expressos em microfarads (μF = 0,000 001 F), nanofarads (nF = 0,000 000 001 F) ou picofarads (0,000 000 000 001 F).

Os capacitores são aplicados em diversas funções em circuitos eletrônicos. Uma das principais é atuar como armazenador de energia em fontes de alimentação, mantendo constante a corrente em um circuito.

Atua também como bloqueio para corrente contínua. Uma vez carregado, a corrente contínua não circula pelo capacitor.

Já a corrente alternada tem livre passagem pelos capacitores. Uma vez que a polaridade inverte-se na velocidade da frequência correspondente, ora uma placa é positiva, ora negativa, fazendo com que o capacitor fique constantemente em processo de carga e descarga.

Observação: Na rede domiciliar temos corrente alternada (110V ou 220V) com frequência de 60Hz. Isso significa que a cada segundo a polaridade do par de condutores é alterada 60 vezes.

Capacitores podem ter seus valores identificados também pelo mesmo código de cores dos resistores. Mais comumente os valores são inscritos nos invólucros desses componentes.

Capacitores variáveis:

Uma categoria importante é a dos capacitores variáveis. Nestes dispositivos, pode-se controlar a área das superfícies condutoras submetidas ao campo elétrico, efetivamente controlando a capacitância. Trimmers e Padders São capacitores variáveis com pequenas dimensões normalmente utilizados em rádios portáteis e em diversos dispositivos eletrônicos. Tem capacitâncias máximas em torno de 500 pF e s ão utilizados principalmente para o ajuste do valor correto da capacitância total de um circuito. O ajuste pode ser feito pela variação da superfície paralela das placas, pela distância entre as placas e pela variação do material do dielétrico. Identificação em capacitores cerâmicos, por cores Identificação em capacitores cerâmicos, por código

Capacitor para "sintonia" Modelos de trimmers

Tempo de Carga e Descarga de um Capacitor

Um capacitor só se carrega instantaneamente se não houver nenhuma resistência no circuito de carga. Havendo resistência em série com o capacitor, haverá uma dificuldade da corrente circular e portanto, a carga total do capacitor somente se dará após determinado período de tempo.

A fórmula para cálculo da constante de tempo em um circuito composto de resistor e capacitor é: t = R . C
onde, t = tempo em segundos, R = a resistência em MegaOhms, C = a capacitância em microfarads.

Exemplo: Para R = 1.000.000 (1M ohm) e C = 0,000 001 (1μF) temos o tempo de 1 segundo para carga do capacitor.

Reatância ou reagência elétrica é a oposição oferecida à passagem de corrente elétrica alternada em um dispositivo indutivo ou capacitivo.

Quando o componente é uma capacitância, diz-se que a corrente elétrica encontra uma resistência à sua passagem, denominada de reatância capacitiva.

A reatância capacitiva é o tipo de reatância devida à capacitância de um capacitor ou de um circuito elétrico. É medida em OHM e é igual à recíproca do produto de "2 . ¶ . f"    ( 2 . 3,14 . frequência) e pela capacitância em farads ou faradays, onde X < 0.

A reatância é capacitiva (XC) e o seu valor em ohms é dado por: Onde C é a capacitância dada em Faradays, f é a freqüência dada em Hertz

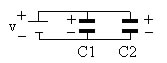
Associação de capacitores

A associação em paralelo é ilustrada na figura ao lado, para o caso de dois capacitores. O que caracteriza esse tipo de associação é a igualdade de potencial entre as placas dos capacitores. Na ilustração, as placas superiores estão com o mesmo potencial, dado pelo pólo positivo da baterial. Da mesma forma, as placas inferiores estão com o mesmo potencial negativo. Portanto, as diferenças de potencial são iguais, i.e., V1=V2=V.

Vimos anteriormente que  C = Q / V    (capacitância = qtde de carga armazenada / voltagem aplicada) e portanto, teremos para os capacitores C1 e C2 acima, que:

Q1 = C1 . V
Q2 = C2 . V

A carga Q fornecida pela bateria é distribuída entre os capacitores na proporção de suas capacidades. Assim  Q=Q1+Q2, ou então:

Q = (C1 . V) + (C2 . V)
Q = (C1 + C2) . V  

Portanto, deduzimos que a capacitância equivalente na associação em paralelo é: Ceq = C1 + C2

No caso mais geral, associando 'n' capacitores, diremos que a capacitância equivalente total é igual a soma das capacitâncias individuais de cada um dos capacitores:

No caso da associação em série vista na figura ao lado, são iguais as cargas acumuladas nas placas de todos os capacitores. Armazenando quantidade igual de carga mas com capacitâncias diferentes, teremos consequentemente diferentes potenciais em cada capacitor do circuito.
Portanto, Q1 = Q2 = Q = C1 . V1 = C2 . V2       e então
A associação em série de capacitores equivalerá a um capacitor equivalente cujo valor é dado por:
Para a associação em série de dois capacitores, teremos a equação simplificada:

Indutores

Indutores são condutores dispostos em forma de espiral nos quais os campos eletromagnéticos formados geram correntes que tendem a se opor às variações das correntes aplicada nos mesmos.

Um indutor é geralmente construído como uma bobina de material condutor, por exemplo, fio de cobre. Um núcleo de material ferromagnético aumenta a indutância concentrando as linhas de força de campo magnético que fluem pelo interior das espiras.

A indutância é a grandeza física associada aos indutores, sendo simbolizada pela letra L, medida em henry (H) e representada graficamente por um fio helicoidal.

Em outras palavras é um parâmetro dos circuitos lineares que relaciona a tensão induzida por um campo magnético variável à corrente responsável pelo campo. A tensão entre os terminais de um indutor é proporcional à taxa de variação da corrente que o atravessa. Matematicamente temos: u(t) = L . i  /  t

onde u(t) é a tensão instântanea, sua unidade de medida é o volt (V), L é a indutância, sua unidade de medida é o henry (H), i é a corrente, sua unidade de medida é o ampère (A) e t o tempo (s).

A energia (medida em Joules) armazenada num indutor é igual à quantidade de trabalho necessária para estabalecer o fluxo de corrente através do indutor e, conseqüentemente, o campo magnético. É dada pela equação ao lado, onde I é a corrente que circula pelo indutor.

Um indutor tende a se opor a variações de corrente. Um indutor ideal não oferece resistência para corrente contínua, exceto quando a corrente é ligada e desligada, caso em que ocorre a variação de intensidade de corrente. Porém, todos os indutores do mundo real são construídos a partir de materiais com resistência elétrica finita (componente resistiva), que se opõe até mesmo à corrente contínua.

Quando uma corrente alternada senoidal flui por um indutor, uma tensão alternada senoidal (ou força eletromotriz) é induzida. A amplitude da força eletromotriz está relacionada com a amplitude da corrente e com a freqüência da onda senoidal, segundo a equação ao lado:
onde "w" corresponde a frequência angular da senoide, sendo definida por:

Reatância ou reagência elétrica é a oposição oferecida à passagem de corrente elétrica alternada em um dispositivo indutivo ou capacitivo.

Quando o componente é uma indutância, diz-se que a corrente elétrica encontra uma resistência à sua passagem, denominada de reatância indutiva.

A unidade de medida da reatância é o OHM. Em um circuito submetido a corrente alternada temos sempre uma combinação de resistência pura com reatâncias, o que constitui a componente chamada Impedância (quando o circuito é indutivo, diz-se que ocorre a impedância indutiva).

A relação entre impedância, resistência e reatância é dada pela equação ao lado: sendo, Z = impedância em OHMs; R a resistência pura do circuito em OHMS; X = reatância em OHMS
No caso de circuito indutivo, temos que a reatância indutiva é definida por: onde XL = reatância indutiva em OHMs, f = frequência da onda senoidal; L= Indutância em Henry

Associação de indutores

Cada indutor de uma configuração em paralelo possui a mesma diferença de potencial (tensão) que os demais. Para encontrar a indutância equivalente total equivalente:

A corrente através de indutores em série permanece a mesma, mas a tensão de cada indutor pode ser diferente. A soma das diferenças de potencial é igual à tensão total. Para encontrar a indutância total:

Fator Q

O fator Q ("fator de mérito") de um indutor pode ser encontrado através desta fórmula, onde R é a resistência elétrica interna do indutor:

O indutor terá maior fator "Q" quanto menor sua resistência pura (fios de maior bitola). Para um mesmo indutor, observa-se que o fator "Q" diminui com a diminuição da frequência ( w = 2 . ¶ . f )

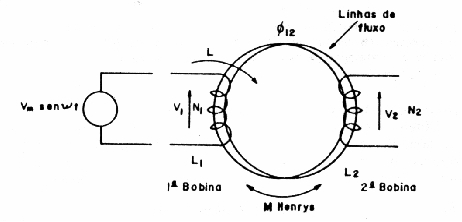
Indutância mútua

Quando a posição indutiva de dois indutores com N1 e N2 espiras e L1 e L2 henry é tal que o fluxo originado num indutor atinge o outro, os dois estão indutivamente associados(acoplamento indutivo), e entre eles existe a indutância mutua (M) medida em henry.

Uma das aplicações da indutância mútua é em transformadores. Aplicando-se uma tensão em um dos indutores haverá a indutância mútua e o aparecimento de tensão nos terminasi do segundo indutor. O transformador poderá ser elevador ou baixador de tensão, dependendo da relação de espiras entre ambos os indutores (número maior de espiras do indutor 2, eleva-se a tensão aplicada no indutor 1).

A relação de espiras entre ambos os indutores dará a relação de tensão entre eles.